Если функция регрессии линейная, то говорят о линейной регрессии . Линейная регрессия находит весьма широкое применение в эконометрике в связи с четкой экономической интерпретации ее параметров. Кроме того, построенное линейное уравнение может служить начальной точкой эконометрического анализа.
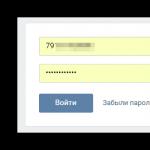
Простая линейная регрессия представляет собой линейную функцию между условным математическим ожиданием зависимой переменной и одной зависимой переменной X (x i – значения зависимой переменной в i -ом наблюдении):
![]() . (5.5)
. (5.5)
Для отражения того факта, что каждое индивидуальное значение y i отклоняется от соответствующего условного математического ожидания, необходимо ввести в соотношение (5.5) случайное слагаемое e i :
![]() . (5.6)
. (5.6)
Это соотношение называется теоретической линейной регрессионной моделью ; b 0 и b 1 – теоретическими коэффициентами регрессии . Таким образом, индивидуальные значения y i представляют в виде двух компонент – систематической () и случайной (e i ). В общем виде теоретическую линейную регрессионную модель будем представлять в виде
![]() . (5.7)
. (5.7)
Основная задача линейного регрессионного анализа состоит в том, чтобы по имеющимся статистическим данным для переменных X и Y получить наилучшие оценки неизвестных параметров b 0 и b 1 . По выборке ограниченного объема можно построить эмпирическое линейное уравнение регрессии :
где – оценка условного математического ожидания ![]() , b
0 и b
1 – оценки неизвестных параметров b 0 и b 1 , называемые эмпирическими коэффициентами регрессии
. Следовательно, в конкретном случае
, b
0 и b
1 – оценки неизвестных параметров b 0 и b 1 , называемые эмпирическими коэффициентами регрессии
. Следовательно, в конкретном случае
![]() , (5.9)
, (5.9)
где отклонение e i – оценка теоретического случайного отклонения e i .
Задача линейного регрессионного анализа состоит в том, чтобы по конкретной выборке (x i
,y i
) найти оценки b
0 и b
1 неизвестных параметров b 0 и b 1 так, чтобы построенная линия регрессии была бы наилучшей в определенном смысле среди всех других прямых. Другими словами, построенная прямая ![]() должна быть «ближайшей» к точкам наблюдений по их совокупности. Мерами качества найденных оценок могут служить определенные композиции отклонений e i
. Например, коэффициенты b
0 и b
1 эмпирического уравнения регрессии могут быть оценены исходя из условия минимизации функции потерь (loss function)
:
должна быть «ближайшей» к точкам наблюдений по их совокупности. Мерами качества найденных оценок могут служить определенные композиции отклонений e i
. Например, коэффициенты b
0 и b
1 эмпирического уравнения регрессии могут быть оценены исходя из условия минимизации функции потерь (loss function)
:  . Например, функции потерь могут быть выбраны в следующем виде:
. Например, функции потерь могут быть выбраны в следующем виде:
1)  ; ;
| 2)  ; ;
| 3) |
Самым распространенным и теоретически обоснованным является метод нахождения коэффициентов, при котором минимизируется первая сумма. Он получил название метод наименьших квадратов (МНК) . Этот метод оценки является наиболее простым с вычислительной точки зрения. Кроме того, оценки коэффициентов регрессии, найденные МНК при определенных предпосылках, обладают рядом оптимальных свойств. Хорошие статистические свойства метода, простота математических выводов делают возможным построить развитую теорию, позволяющую провести тщательную проверку различных статистических гипотез. Минусы метода – чувствительность в «выбросам».
Метод определения оценок коэффициентов из условия минимизации второй суммы называется методом наименьших модулей . Этот метод обладает определенными достоинствами, например, по сравнению с методом наименьших квадратов он нечувствителен к выбросам (обладает робастностью). Однако у него имеются существенные недостатки. В первую очередь это связано со сложностью вычислительных процедур. Во-вторых, с неоднозначностью метода, т.е. разным значениям коэффициентов регрессии могут соответствовать одинаковые суммы модулей отклонений.
Метод минимизации максимума модуля отклонения наблюдаемого значения результативного показателя y i от модельного значения называется методом минимакса , а получаемая при этом регрессия минимаксной .
Среди других методов оценивания коэффициентов регрессии отметим метод максимального правдоподобия (ММП) .
В предыдущих заметках предметом анализа часто становилась отдельная числовая переменная, например, доходность взаимных фондов, время загрузки Web-страницы или объем потребления безалкогольных напитков. В настоящей и следующих заметках мы рассмотрим методы предсказания значений числовой переменной в зависимости от значений одной или нескольких других числовых переменных.
Материал будет проиллюстрирован сквозным примером. Прогнозирование объема продаж в магазине одежды. Сеть магазинов уцененной одежды Sunflowers на протяжении 25 лет постоянно расширялась. Однако в настоящее время у компании нет систематического подхода к выбору новых торговых точек. Место, в котором компания собирается открыть новый магазин, определяется на основе субъективных соображений. Критериями выбора являются выгодные условия аренды или представления менеджера об идеальном местоположении магазина. Представьте, что вы - руководитель отдела специальных проектов и планирования. Вам поручили разработать стратегический план открытия новых магазинов. Этот план должен содержать прогноз годового объема продаж во вновь открываемых магазинах. Вы полагаете, что торговая площадь непосредственно связана с объемом выручки, и хотите учесть этот факт в процессе принятия решения. Как разработать статистическую модель, позволяющую прогнозировать годовой объем продаж на основе размера нового магазина?
Как правило, для предсказания значений переменной используется регрессионный анализ. Его цель - разработать статистическую модель, позволяющую предсказывать значения зависимой переменной, или отклика, по значениям, по крайней мере одной, независимой, или объясняющей, переменной. В настоящей заметке мы рассмотрим простую линейную регрессию - статистический метод, позволяющий предсказывать значения зависимой переменной Y по значениям независимой переменной X . В последующих заметках будет описана модель множественной регрессии, предназначенная для предсказания значений независимой переменной Y по значениям нескольких зависимых переменных (Х 1 , Х 2 , …, X k ).
Скачать заметку в формате или , примеры в формате
Виды регрессионных моделей
где ρ 1 – коэффициент автокорреляции; если ρ 1 = 0 (нет автокорреляции), D ≈ 2; если ρ 1 ≈ 1 (положительная автокорреляции), D ≈ 0; если ρ 1 = -1 (отрицательная автокорреляции), D ≈ 4.
На практике применение критерия Дурбина-Уотсона основано на сравнении величины D с критическими теоретическими значениями d L и d U для заданного числа наблюдений n , числа независимых переменных модели k (для простой линейной регрессии k = 1) и уровня значимости α. Если D < d L , гипотеза о независимости случайных отклонений отвергается (следовательно, присутствует положительная автокорреляция); если D > d U , гипотеза не отвергается (то есть автокорреляция отсутствует); если d L < D < d U , нет достаточных оснований для принятия решения. Когда расчётное значение D превышает 2, то с d L и d U сравнивается не сам коэффициент D , а выражение (4 – D ).
Для вычисления статистики Дурбина-Уотсона в Excel обратимся к нижней таблице на рис. 14 Вывод остатка . Числитель в выражении (10) вычисляется с помощью функции =СУММКВРАЗН(массив1;массив2), а знаменатель =СУММКВ(массив) (рис. 16).

Рис. 16. Формулы расчета статистики Дурбина-Уотсона
В нашем примере D = 0,883. Основной вопрос заключается в следующем - какое значение статистики Дурбина-Уотсона следует считать достаточно малым, чтобы сделать вывод о существовании положительной автокорреляции? Необходимо соотнести значение D с критическими значениями (d L и d U ), зависящими от числа наблюдений n и уровня значимости α (рис. 17).

Рис. 17. Критические значения статистики Дурбина-Уотсона (фрагмент таблицы)
Таким образом, в задаче об объеме продаж в магазине, доставляющем товары на дом, существуют одна независимая переменная (k = 1), 15 наблюдений (n = 15) и уровень значимости α = 0,05. Следовательно, d L = 1,08 и d U = 1,36. Поскольку D = 0,883 < d L = 1,08, между остатками существует положительная автокорреляция, метод наименьших квадратов применять нельзя.
Проверка гипотез о наклоне и коэффициенте корреляции
Выше регрессия применялась исключительно для прогнозирования. Для определения коэффициентов регрессии и предсказания значения переменной Y при заданной величине переменной X использовался метод наименьших квадратов. Кроме того, мы рассмотрели среднеквадратичную ошибку оценки и коэффициент смешанной корреляции. Если анализ остатков подтверждает, что условия применимости метода наименьших квадратов не нарушаются, и модель простой линейной регрессии является адекватной, на основе выборочных данных можно утверждать, что между переменными в генеральной совокупности существует линейная зависимость.
Применение t -критерия для наклона. Проверяя, равен ли наклон генеральной совокупности β 1 нулю, можно определить, существует ли статистически значимая зависимость между переменными X и Y . Если эта гипотеза отклоняется, можно утверждать, что между переменными X и Y существует линейная зависимость. Нулевая и альтернативная гипотезы формулируются следующим образом: Н 0: β 1 = 0 (нет линейной зависимости), Н1: β 1 ≠ 0 (есть линейная зависимость). По определению t -статистика равна разности между выборочным наклоном и гипотетическим значением наклона генеральной совокупности, деленной на среднеквадратичную ошибку оценки наклона:
(11) t = (b 1 – β 1 ) / S b 1
где b
1
– наклон прямой регрессии по выборочным данным, β1 – гипотетический наклон прямой генеральной совокупности, ![]() , а тестовая статистика t
имеет t
-распределение с n – 2
степенями свободы.
, а тестовая статистика t
имеет t
-распределение с n – 2
степенями свободы.
Проверим, существует ли статистически значимая зависимость между размером магазина и годовым объемом продаж при α = 0,05. t -критерий выводится наряду с другими параметрами при использовании Пакета анализа (опция Регрессия ). Полностью результаты работы Пакета анализа приведены на рис. 4, фрагмент, относящийся к t-статистике – на рис. 18.
Рис. 18. Результаты применения t
Поскольку число магазинов n = 14 (см. рис.3), критическое значение t -статистики при уровне значимости α = 0,05 можно найти по формуле: t L =СТЬЮДЕНТ.ОБР(0,025;12) = –2,1788, где 0,025 – половина уровня значимости, а 12 = n – 2; t U =СТЬЮДЕНТ.ОБР(0,975;12) = +2,1788.
Поскольку t -статистика = 10,64 > t U = 2,1788 (рис. 19), нулевая гипотеза Н 0 отклоняется. С другой стороны, р -значение для Х = 10,6411, вычисляемое по формуле =1-СТЬЮДЕНТ.РАСП(D3;12;ИСТИНА), приближенно равно нулю, поэтому гипотеза Н 0 снова отклоняется. Тот факт, что р -значение почти равно нулю, означает, что если бы между размерами магазинов и годовым объемом продаж не существовало реальной линейной зависимости, обнаружить ее с помощью линейной регрессии было бы практически невозможно. Следовательно, между средним годовым объемом продаж в магазинах и их размером существует статистически значимая линейная зависимость.

Рис. 19. Проверка гипотезы о наклоне генеральной совокупности при уровне значимости, равном 0,05, и 12 степенях свободы
Применение F -критерия для наклона. Альтернативным подходом к проверке гипотез о наклоне простой линейной регрессии является использование F -критерия. Напомним, что F -критерий применяется для проверки отношения между двумя дисперсиями (подробнее см. ). При проверке гипотезы о наклоне мерой случайных ошибок является дисперсия ошибки (сумма квадратов ошибок, деленная на количество степеней свободы), поэтому F -критерий использует отношение дисперсии, объясняемой регрессией (т.е. величины SSR , деленной на количество независимых переменных k ), к дисперсии ошибок (MSE = S Y X 2 ).
По определению F -статистика равна среднему квадрату отклонений, обусловленных регрессией (MSR), деленному на дисперсию ошибки (MSE): F = MSR / MSE , где MSR = SSR / k , MSE = SSE /(n – k – 1), k – количество независимых переменных в регрессионной модели. Тестовая статистика F имеет F -распределение с k и n – k – 1 степенями свободы.
При заданном уровне значимости α решающее правило формулируется так: если F > F U , нулевая гипотеза отклоняется; в противном случае она не отклоняется. Результаты, оформленные в виде сводной таблицы дисперсионного анализа, приведены на рис. 20.

Рис. 20. Таблица дисперсионного анализа для проверки гипотезы о статистической значимости коэффициента регрессии
Аналогично t -критерию F -критерий выводится в таблицу при использовании Пакета анализа (опция Регрессия ). Полностью результаты работы Пакета анализа приведены на рис. 4, фрагмент, относящийся к F -статистике – на рис. 21.

Рис. 21. Результаты применения F -критерия, полученные с помощью Пакета анализа Excel
F-статистика равна 113,23, а р -значение близко к нулю (ячейка Значимость F ). Если уровень значимости α равен 0,05, определить критическое значение F -распределения с одной и 12 степенями свободы можно по формуле F U =F.ОБР(1-0,05;1;12) = 4,7472 (рис. 22). Поскольку F = 113,23 > F U = 4,7472, причем р -значение близко к 0 < 0,05, нулевая гипотеза Н 0 отклоняется, т.е. размер магазина тесно связан с его годовым объемом продаж.

Рис. 22. Проверка гипотезы о наклоне генеральной совокупности при уровне значимости, равном 0,05, с одной и 12 степенями свободы
Доверительный интервал, содержащий наклон β 1 . Для проверки гипотезы о существовании линейной зависимости между переменными можно построить доверительный интервал, содержащий наклон β 1 и убедиться, что гипотетическое значение β 1 = 0 принадлежит этому интервалу. Центром доверительного интервала, содержащего наклон β 1 , является выборочный наклон b 1 , а его границами - величины b 1 ± t n –2 S b 1
Как показано на рис. 18, b 1 = +1,670, n = 14, S b 1 = 0,157. t 12 =СТЬЮДЕНТ.ОБР(0,975;12) = 2,1788. Следовательно, b 1 ± t n –2 S b 1 = +1,670 ± 2,1788 * 0,157 = +1,670 ± 0,342, или + 1,328 ≤ β 1 ≤ +2,012. Таким образом, наклон генеральной совокупности с вероятностью 0,95 лежит в интервале от +1,328 до +2,012 (т.е. от 1 328 000 до 2 012 000 долл.). Поскольку эти величины больше нуля, между годовым объемом продаж и площадью магазина существует статистически значимая линейная зависимость. Если бы доверительный интервал содержал нуль, между переменными не было бы зависимости. Кроме того, доверительный интервал означает, что каждое увеличение площади магазина на 1 000 кв. футов приводит к увеличению среднего объема продаж на величину от 1 328 000 до 2 012 000 долларов.
Использование t -критерия для коэффициента корреляции. был введен коэффициент корреляции r , представляющий собой меру зависимости между двумя числовыми переменными. С его помощью можно установить, существует ли между двумя переменными статистически значимая связь. Обозначим коэффициент корреляции между генеральными совокупностями обеих переменных символом ρ. Нулевая и альтернативная гипотезы формулируются следующим образом: Н 0 : ρ = 0 (нет корреляции), Н 1 : ρ ≠ 0 (есть корреляция). Проверка существования корреляции:

где r = + , если b 1 > 0, r = – , если b 1 < 0. Тестовая статистика t имеет t -распределение с n – 2 степенями свободы.
В задаче о сети магазинов Sunflowers r 2 = 0,904, а b 1 - +1,670 (см. рис. 4). Поскольку b 1 > 0, коэффициент корреляции между объемом годовых продаж и размером магазина равен r = +√0,904 = +0,951. Проверим нулевую гипотезу, утверждающую, что между этими переменными нет корреляции, используя t -статистику:

При уровне значимости α = 0,05 нулевую гипотезу следует отклонить, поскольку t = 10,64 > 2,1788. Таким образом, можно утверждать, что между объемом годовых продаж и размером магазина существует статистически значимая связь.
При обсуждении выводов, касающихся наклона генеральной совокупности, доверительные интервалы и критерии для проверки гипотез являются взаимозаменяемыми инструментами. Однако вычисление доверительного интервала, содержащего коэффициент корреляции, оказывается более сложным делом, поскольку вид выборочного распределения статистики r зависит от истинного коэффициента корреляции.
Оценка математического ожидания и предсказание индивидуальных значений
В этом разделе рассматриваются методы оценки математического ожидания отклика Y и предсказания индивидуальных значений Y при заданных значениях переменной X .
Построение доверительного интервала. В примере 2 (см. выше раздел Метод наименьших квадратов ) регрессионное уравнение позволило предсказать значение переменной Y X . В задаче о выборе места для торговой точки средний годовой объем продаж в магазине площадью 4000 кв. футов был равен 7,644 млн. долл. Однако эта оценка математического ожидания генеральной совокупности является точечной. для оценки математического ожидания генеральной совокупности была предложена концепция доверительного интервала. Аналогично можно ввести понятие доверительного интервала для математического ожидания отклика при заданном значении переменной X :
где  , =
b
0
+
b
1
X i
– предсказанное значение переменное Y
при X
= X i
, S YX
– среднеквадратичная ошибка, n
– объем выборки, X
i
- заданное значение переменной X
, µ
Y
| X
=
X
i
– математическое ожидание переменной Y
при Х
= Х i
, SSX =
, =
b
0
+
b
1
X i
– предсказанное значение переменное Y
при X
= X i
, S YX
– среднеквадратичная ошибка, n
– объем выборки, X
i
- заданное значение переменной X
, µ
Y
| X
=
X
i
– математическое ожидание переменной Y
при Х
= Х i
, SSX = 
Анализ формулы (13) показывает, что ширина доверительного интервала зависит от нескольких факторов. При заданном уровне значимости возрастание амплитуды колебаний вокруг линии регрессии, измеренное с помощью среднеквадратичной ошибки, приводит к увеличению ширины интервала. С другой стороны, как и следовало ожидать, увеличение объема выборки сопровождается сужением интервала. Кроме того, ширина интервала изменяется в зависимости от значений X i . Если значение переменной Y предсказывается для величин X , близких к среднему значению , доверительный интервал оказывается уже, чем при прогнозировании отклика для значений, далеких от среднего.
Допустим, что, выбирая место для магазина, мы хотим построить 95%-ный доверительный интервал для среднего годового объема продаж во всех магазинах, площадь которых равна 4000 кв. футов:

Следовательно, средний годовой объем продаж во всех магазинах, площадь которых равна 4 000 кв. футов, с 95% -ной вероятностью лежит в интервале от 6,971 до 8,317 млн. долл.
Вычисление доверительного интервала для предсказанного значения. Кроме доверительного интервала для математического ожидания отклика при заданном значении переменной X , часто необходимо знать доверительный интервал для предсказанного значения. Несмотря на то что формула для вычисления такого доверительного интервала очень похожа на формулу (13), этот интервал содержит предсказанное значение, а не оценку параметра. Интервал для предсказанного отклика Y X = Xi при конкретном значении переменной X i определяется по формуле:

Предположим, что, выбирая место для торговой точки, мы хотим построить 95%-ный доверительный интервал для предсказанного годового объема продаж в магазине, площадь которого равна 4000 кв. футов:

Следовательно, предсказанный годовой объем продаж в магазине, площадь которого равна 4000 кв. футов, с 95%-ной вероятностью лежит в интервале от 5,433 до 9,854 млн. долл. Как видим, доверительный интервал для предсказанного значения отклика намного шире, чем доверительный интервал для его математического ожидания. Это объясняется тем, что изменчивость при прогнозировании индивидуальных значений намного больше, чем при оценке математического ожидания.
Подводные камни и этические проблемы, связанные с применением регрессии
Трудности, связанные с регрессионным анализом:
- Игнорирование условий применимости метода наименьших квадратов.
- Ошибочная оценка условий применимости метода наименьших квадратов.
- Неправильный выбор альтернативных методов при нарушении условий применимости метода наименьших квадратов.
- Применение регрессионного анализа без глубоких знаний о предмете исследования.
- Экстраполяция регрессии за пределы диапазона изменения объясняющей переменной.
- Путаница между статистической и причинно-следственной зависимостями.
Широкое распространение электронных таблиц и программного обеспечения для статистических расчетов ликвидировало вычислительные проблемы, препятствовавшие применению регрессионного анализа. Однако это привело к тому, что регрессионный анализ стали применять пользователи, не обладающие достаточной квалификацией и знаниями. Откуда пользователям знать об альтернативных методах, если многие из них вообще не имеют ни малейшего понятия об условиях применимости метода наименьших квадратов и не умеют проверять их выполнение?
Исследователь не должен увлекаться перемалыванием чисел - вычислением сдвига, наклона и коэффициента смешанной корреляции. Ему нужны более глубокие знания. Проиллюстрируем это классическим примером, взятым из учебников. Анскомб показал, что все четыре набора данных, приведенных на рис. 23, имеют одни и те же параметры регрессии (рис. 24).

Рис. 23. Четыре набора искусственных данных

Рис. 24. Регрессионный анализ четырех искусственных наборов данных; выполнен с помощью Пакета анализа (кликните на рисунке, чтобы увеличить изображение)
Итак, с точки зрения регрессионного анализа все эти наборы данных совершенно идентичны. Если бы анализ был на этом закончен, мы потеряли бы много полезной информации. Об этом свидетельствуют диаграммы разброса (рис. 25) и графики остатков (рис. 26), построенные для этих наборов данных.

Рис. 25. Диаграммы разброса для четырех наборов данных
Диаграммы разброса и графики остатков свидетельствуют о том, что эти данные отличаются друг от друга. Единственный набор, распределенный вдоль прямой линии, - набор А. График остатков, вычисленных по набору А, не имеет никакой закономерности. Этого нельзя сказать о наборах Б, В и Г. График разброса, построенный по набору Б, демонстрирует ярко выраженную квадратичную модель. Этот вывод подтверждается графиком остатков, имеющим параболическую форму. Диаграмма разброса и график остатков показывают, что набор данных В содержит выброс. В этой ситуации необходимо исключить выброс из набора данных и повторить анализ. Метод, позволяющий обнаруживать и исключать выбросы из наблюдений, называется анализом влияния. После исключения выброса результат повторной оценки модели может оказаться совершенно иным. Диаграмма разброса, построенная по данным из набора Г, иллюстрирует необычную ситуацию, в которой эмпирическая модель значительно зависит от отдельного отклика (Х 8 = 19, Y 8 = 12,5). Такие регрессионные модели необходимо вычислять особенно тщательно. Итак, графики разброса и остатков являются крайне необходимым инструментом регрессионного анализа и должны быть его неотъемлемой частью. Без них регрессионный анализ не заслуживает доверия.

Рис. 26. Графики остатков для четырех наборов данных
Как избежать подводных камней при регрессионном анализе:
- Анализ возможной взаимосвязи между переменными X и Y всегда начинайте с построения диаграммы разброса.
- Прежде чем интерпретировать результаты регрессионного анализа, проверяйте условия его применимости.
- Постройте график зависимости остатков от независимой переменной. Это позволит определить, насколько эмпирическая модель соответствует результатам наблюдения, и обнаружить нарушение постоянства дисперсии.
- Для проверки предположения о нормальном распределении ошибок используйте гистограммы, диаграммы «ствол и листья», блочные диаграммы и графики нормального распределения.
- Если условия применимости метода наименьших квадратов не выполняются, используйте альтернативные методы (например, модели квадратичной или множественной регрессии).
- Если условия применимости метода наименьших квадратов выполняются, необходимо проверить гипотезу о статистической значимости коэффициентов регрессии и построить доверительные интервалы, содержащие математическое ожидание и предсказанное значение отклика.
- Избегайте предсказывать значения зависимой переменной за пределами диапазона изменения независимой переменной.
- Имейте в виду, что статистические зависимости не всегда являются причинно-следственными. Помните, что корреляция между переменными не означает наличия причинно-следственной зависимости между ними.
Резюме. Как показано на структурной схеме (рис. 27), в заметке описаны модель простой линейной регрессии, условия ее применимости и способы проверки этих условий. Рассмотрен t -критерий для проверки статистической значимости наклона регрессии. Для предсказания значений зависимой переменной использована регрессионная модель. Рассмотрен пример, связанный с выбором места для торговой точки, в котором исследуется зависимость годового объема продаж от площади магазина. Полученная информация позволяет точнее выбрать место для магазина и предсказать его годовой объем продаж. В следующих заметках будет продолжено обсуждение регрессионного анализа, а также рассмотрены модели множественной регрессии.

Рис. 27. Структурная схема заметки
Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 792–872
Если зависимая переменная является категорийной, необходимо применять логистическую регрессию.
Парная (простая) линейная регрессия представляет собой модель, где среднее значение зависимой (объясняемой) переменной рассматривается как функция одной независимой (объясняющей) переменной x , т.е. это модель вида:
Так же y называют результативным признаком, а x признаком-фактором.
Знак «^» означает, что между переменными x и y нет строгой функциональной зависимости. Практически в каждом отдельном случае величина y складывается из двух слагаемых:
![]() (4.5)
(4.5)
где y – фактическое значение результативного признака;
– теоретическое значение результативного признака, найденное исходя из уравнения регрессии;
e – случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.
Случайная величина e включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели порождено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных.
Различают линейные и нелинейные регрессии.
Линейная регрессия: y = a + b × x + e .
Нелинейные регрессии делятся на два класса:
ü регрессии,нелинейныеотносительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;
ü регрессии, нелинейные по оцениваемым параметрам.
Например:
ü регрессии, нелинейные по объясняющим переменным :
полиномы разных степеней y = a + b × x + b × x 2 + ... + b × x n + e ;
равностронняя гипербола y = a + b /x + e ;
ü регрессии, нелинейные по оцениваемым параметрам :
степенная y = a × x b × e ;
Показательная y = a × b x ×e ;
Экспоненциальная y = e a + bx +e .
Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такиеоценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака y от теоретических минимальна, т.е.
![]() (4.6)
(4.6)
Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно a и b :
 (4.7)
(4.7)
Можно воспользоваться готовыми формулами, которые вытекают непосредственно из решения этой системы:
 (4.8)
(4.8)
где – ковариация признаков x и y,
– дисперсия признака x и
(Ковариация – числовая характеристика совместного распределения двух случайных величин, равная математическому ожиданию произведения отклонений этих случайных величин от их математических ожиданий. Дисперсия – характеристика случайной величины, определяемая как математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Математическое ожидание – сумма произведений значений случайной величины на соответствующие вероятности.)
Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции r xy для линейной регрессии(-1£ r xy £1):
 (4.9)
(4.9)
и индекс корреляции r xy – для нелинейной регрессии(0£ r xy £ 1):
 (4.10)
(4.10)
где ![]() –
общая дисперсия результативного признака у
;
–
общая дисперсия результативного признака у
;
![]() –
остаточная дисперсия, определяемая исходя из уравнения регрессии
–
остаточная дисперсия, определяемая исходя из уравнения регрессии
Оценку качества построенной модели даст коэффициент (индекс) детерминации r 2 (для линейной регрессии) либо r 2 (для нелинейной регрессии), а также средняя ошибка аппроксимации.
Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических:
 (4.11)
(4.11)
Допустимый предел значений – не более 10%.
Средний коэффициент эластичности показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на1%от своего среднего значения:
![]() (4.12)
(4.12)
После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом,так и отдельных егопараметров.
Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.
Оценка значимости уравнения регрессии в целом производится на основе F -критерия Фишера , которому предшествует дисперсионный анализ. Согласно основной идее дисперсионного анализа, общая сумма квадратов отклонений переменной y от среднего значения y раскладывается на две части – « объясненную » и «необъясненную »:
где ∑(y - ) 2 – общая сумма квадратов отклонений;
( - ) 2 – сумма квадратов отклонений, объясненная регрессией (или факторная сумма квадратов отклонений);
∑(y – ) 2 – остаточная сумма квадратов отклонений, характеризующая влияние неучтенных в модели факторов.
Схема дисперсионного анализа имеет вид, представленный в табл. 4.1 (n – число наблюдений, m – число параметров при переменной x ).
Таблица 4.1

Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду (напомним, что степени свободы – это числа, показывающие количество элементов варьирования, которые могут принимать произвольные значения, не изменяющие заданных характеристик). Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F -критерия Фишера:
Фактическое значение F -критерия Фишера сравнивается с табличным значением F табл (a ; k 1 ; k 2) при уровне значимости a и степенях свободы k 1 = m и k 2 = n - m - 1. При этом, если фактическое значение F -критерия больше табличного, то признается статистическая значимость уравнения в целом.
Для парной линейной регрессии m = 1, поэтому
 (4.15)
(4.15)
Величина F -критерия связана с коэффициентом детерминации r xy 2 , и ее можно рассчитать по следующей формуле:
 (4.16)
(4.16)
Для оценки статистической значимости параметров регрессии и корреляции рассчитываются t -критерий Стьюдента и доверительные интервалы каждого из показателей.Оценка значимости коэффициентоврегрессии и корреляции с помощью t -критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:
 (4.17)
(4.17)
Стандартные ошибки параметров линейной регрессии икоэффициента корреляции определяются по формулам:
|

Сравнивая фактическое и критическое (табличное) значения t - статистики – t табл и t факт – делаем вывод о значимости параметров регрессии и корреляции. Если t табл < t факт то параметры a , b и r xy не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора x. Если t табл > t факт , то признается случайная природа формирования a , b или r xy .
Для расчета доверительного интервала определяем предельную ошибку ∆для каждого показателя:
Формулы для расчета доверительных интервалов имеют следующий вид:

Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.
Связь между F -критерием Фишера и t -статистикой Стьюдента выражается равенством
![]()
В прогнозных расчетах по уравнению регрессии определяется предсказываемое индивидуальное значение y 0 как точечный прогноз при x = x 0 ,т.е.путем подстановки в линейное уравнение = a + b × x соответствующего значения x. Однако точечный прогноз явно нереален, поэтому он дополняется расчетом стандартной ошибки
 (4.19)
(4.19)
где  , и построением доверительного интервала
прогнозного значения :
, и построением доверительного интервала
прогнозного значения :
C помощью инструмента анализа данных Регрессия можно получить результаты регрессионной статистики, дисперсионного анализа, доверительных интервалов, остатки и графики подбора линии регрессии.
Если в меню сервис еще нет команды Анализ данных , то необходимо сделать следующее. В главном меню последовательно выбираем Сервис→Надстройки и устанавливаем «флажок» в строке Пакет анализа (рис. 4.1).
1. Если исходные данные уже внесены, то выбираем Сервис→Анализ данных→Регрессия .
2. Заполняем диалоговое окно ввода данных и параметров вывода (рис. 4.2).
Входной интервал Y –диапазон,содержащий данныерезультативного признака;
Входной интервал X –диапазон,содержащий данные признака-фактора;
Метки – «флажок»,который указывает,содержит ли первая строканазвания столбцов;
Рис. 4.1. Строка Пакет анализа
Рис. 4.2. Диалоговое окно ввода данных и параметров вывода
Константа – ноль – «флажок»,указывающий на наличие илиотсутствие свободного члена в уравнении;
Выходной интервал –достаточно указать левую верхнюю ячейкубудущего диапазона;
Новый рабочий лист –можно указать произвольное имя новоголиста (или не указывать, тогда результаты выводятся на вновь созданный лист).
Получаем подобные результаты:
Откуда выписываем, округляя до 4 знаков после запятой и переходя к нашим обозначениям:
Уравнение регрессии:
76,9765+0,9204x .
Коэффициент корреляции:
r xy =0,7210.
Коэффициент детерминации:
r xy 2 =0,5199.
Фактическое значение F -критерия Фишера:
F =10,8280
Остаточная дисперсия на одну степень свободы:
S ост 2 =157, 4922.
Корень квадратный из остаточной дисперсии (стандартная ошибка):
S ост =12,5496.
Стандартные ошибки для параметров регрессии:
m a =24, 2116 , m b =0, 2797.
Фактические значения t -критерия Стьюдента:
t a =3,1793, t b =3,2906.
Доверительные интервалы:
23,0298 £ a * £130,9232,
0,2972 £ b * £ ,5437.
Как видим, найдены все рассмотренные выше параметры и характеристики уравнения регрессии, за исключением средней ошибки аппроксимации (значение t -критерия Стьюдента для коэффициента корреляции совпадает с t b ). Результаты «ручного счета» от машинного отличаются незначительно (отличия связаны с ошибками округления).
4.3. Финансовое моделирование в Excel.
Начиная создавать финансовую модель предприятия, лучше руководствоваться принципом «от простого к сложному», иначе в попытке учесть все нюансы есть риск запутаться в большом количестве формул и ссылок. Поэтому вполне оправдано вначале создать простейшую модель (с минимальным количеством элементов), установить связи общего характера между внешними параметрами (спрос на продукцию, стоимость ресурсов) и внутренними показателями деятельности предприятия (выручка, затраты, денежные потоки и т. д.). В первой итерации можно не заботиться об особой точности задаваемых параметров. На этом этапе важнее установить правильные взаимосвязи между переменными так, чтобы финансовая модель предприятия автоматически пересчитывалась после изменения исходных данных и позволяла выстраивать различные сценарии. Уже после этого можно приступить к ее развитию, детализовать показатели, ввести дополнительные уровни аналитики и т. д.
1) Доходы. Построение финансовой модели в Excel начинается с задания внешних параметров. Отправной точкой для дальнейших расчетов послужит план продаж. ля этого в Excel на одном из листов книги размещается таблица с планом продаж в денежном выражении (табл. 4.1). На этом этапе выручку можно указать «навскидку» или использовать данные прошлого года. Пока точность не имеет большого значения. Позднее при детализации модели план продаж придется доработать.
2) Расходы. Исходя из объема продаж, определяется размер переменных затрат. В самом общем виде расчет может выглядеть следующим образом:
Переменные затраты = Доля в выручке х Объем продаж
Сделаем небольшое допущение и предположим, что в примере переменными являются только затраты на оплату труда – заработная плата сотрудников полностью зависит от объема оказанных услуг, на нее уходит примерно 30 процентов выручки от реализации. Кстати, план затрат удобнее разместить на отдельном листе Excel (табл. 4.2). В нем зарплата рассчитывается помесячно как произведение коэффициента 0,3 (30% / 100%) и плана продаж на определенный месяц. Расходы на аренду и управление вводятся на первом этапе создания финансовой модели предприятия не как расчетные величины, а как фиксированные значения. В дальнейшем при детализации модели их можно будет заменить формулами, увязав с другими показателями.
Таблица 4.1
План продаж в финансовой модели предприятия, тыс. руб.

Таблица 4.2
План затрат в финансовой модели предприятия, тыс. руб.

Не стоит перегружать планы верхнего уровня (баланс, прибыли и убытки, движение денежных средств) показателями. Лучше стремиться к тому, чтобы каждый из них мог уместиться на одном печатном листе. Зачастую трудно удержаться от соблазна расшифровать каждую цифру (например, в плане доходов и расходов расписать выручку по видам продукции, группам клиентов, каналам сбыта и т. п.). Если в план доходов и расходов включить сотню видов готовой продукции и статей затрат, это значительно затруднит его восприятие. Тем не менее с точки зрения информативности полезно подобные планы дополнять различными относительными показателями (например, в баланс внести показатели структуры активов и пассивов (удельные веса статей в валюте баланса), в план доходов и расходов – рентабельность).
В плане доходов и расходов (табл. 4.3) строки «Операционные расходы» и «Операционные доходы» заполняются при помощи ссылок на соответствующие ячейки функциональных планов. Выручка расшифрована по видам услуг, затраты – по статьям. В этом случае такая расшифровка допустима, поскольку не утяжеляет восприятие отчета и не усложняет его анализ. Кроме того, в отчет включены два аналитических показателя – рентабельность (как отношение прибыли к выручке) и прибыль нарастающим итогом. Если понадобится провести более глубокий анализ, в частности, динамики доли оплаты труда в себестоимости услуг, все необходимые для этого расчеты лучше проводить на отдельном листе.
Таблица 4.3
План доходов и расходов в финансовой модели предприятия, тыс. руб.

План движения денежных средств (табл. 4.4) в нашем примере формируется со следующими допущениями.
Таблица 4.4
План движения денежных средств, тыс. руб.

Первое: разделы «Финансовая деятельность» и «Инвестиционная деятельность» исключены из плана. Предполагается, что предприятие осуществляет только операционную деятельность, не привлекая заемные средства и не осуществляя капитальные вложения. Еще одно допущение. Предприятие оказывает услуги физическим лицам за наличный расчет, а значит, время оказания услуги и ее оплаты совпадает – в итоге у предприятия нет дебиторской задолженности. Ситуация с платежами по операционной деятельности не так однозначна. Зарплата и аренда выплачиваются в месяце, следующем за месяцем начисления, а управленческие расходы – в месяце их осуществления.Последнее, что остается сделать, – создать прогнозный баланс (табл. 4.5). Данные по оборотам за период берутся из ПДР и ПДДС, начальные остатки – из баланса за предыдущий период (здесь допустимо ручное внесение информации).
Таблица 4.5
Прогнозный баланс, тыс. руб.

Построенная таким образом финансовая модель обозначает основные группы показателей, характеризующих деятельность предприятия (доходы, расходы, денежные средства и т. п.), увязывает их в три сводных плана. Даже эту простейшую на первый взгляд модель можно использовать для сценарного анализа. В частности, если исключить из плана продаж услугу № 1(соответствующую строку удалять не нужно, достаточно проставить по ней нули), то можно увидеть, насколько ухудшатся показатели рентабельности и ликвидности.
Чтобы превратить модель в полноценный инструмент сценарного анализа, потребуется «насытить» ее аналитикой, детализировать исходную информацию до показателей, которыми можно управлять на практике. Например, в случае с предприятием, оказывающим услуги, очевидна необходимость детализации плана продаж, внесенного ранее в модель в денежном выражении. Выручку по каждому виду услуг можно рассчитать как произведение цены единицы услуги и количества указанных услуг. На практике, естественно, план продаж формируется исходя из конъюнктуры рынка, ожидаемого спроса, предполагаемой цены реализации, достигнутых договоренностей с ключевыми клиентами, запланированных маркетинговых мероприятий, ценовой и кредитной политики и т. д.
Аналогично детализируются и другие исходные данные. Например, арендную плату можно было бы разложить на площадь арендуемого помещения и стоимость одного квадратного метра, зарплату расписать по сотрудникам, управленческие расходы разбить по видам. В итоге функциональность финансовой модели предприятия развивается до такого уровня, что можно увидеть, как влияет изменение любого, даже самого незначительного параметра на конечный результат.
Сверстать подробную финансовую модель предприятия – задача интересная, но сложная. Потребуется скрупулезно изучить и адекватно математически описать существующие взаимосвязи как внутрипроизводственных процессов, так и внешних факторов. Силами одной финансовой службы такую модель не сделать, понадобится участие всех служб предприятия – от департамента продаж до бухгалтерии.
Использование финансовой модели при планировании деятельности помогает увидеть, как те или иные планы развития отражаются на структуре активов, пассивов, доходов и расходов предприятия, а также определить, от каких факторов в наибольшей степени зависят будущая прибыль, ликвидность и финансовая устойчивость. Модель служит скорее инструментом мониторинга текущей ситуации на предприятии и выработки адекватной финансовой политики.
Финансовую модель предприятия стоит использовать в процессе бюджетирования сразу же после утверждения плана продаж. Если план продаж «прогнать» через модель, то полученный финансовый результат можно показать акционерам, чтобы установить целевые значения по затратам, прибыли, дивидендам. Если планируемая выручка не обеспечивает необходимой прибыли с точки зрения акционеров, прямо в модели корректируются влияющие показатели. Окончательный вариант расчетов модели определяет целевые значения бюджетных лимитов для всех центров финансовой ответственности. В течение года финансовую модель предпредприятия можно будет корректировать, проставлять по пройденным месяцам фактические данные вместо плановых и контролировать таким образом финансовые результаты, отслеживать негативные тенденции и четко понимать, к чему они приведут предприятие.
Финансовая модель в Excel дает возможность:
Спланировать деятельность по проекту, внести ясность в соотношение его эффективности и планируемых затрат на его реализацию;
Проанализировать финансовые показатели проекта, такие как как NPV, IRR, PBP, WACC и др.;
Вводить и анализировать любые изменения в проект.
К преимуществам использования моделирования в Excel относится то, что получаемая финансовая модель гибка и понятна. Вы с любой момент можете посмотреть формулу расчета того или иного показателя и изменять исходные данные проекта по своему усмотрению. Еще одно преимущество построения финансовой модели в Excel - то, что все расчеты идут последовательно и обоснованно.
Для построения финансовой модели в Excel необходима следующая информация по проекту:
Баланс компании на последнюю отчетную дату;
Список продуктов, цены, объем продаж, способы оплаты;
Перечень издержек компании, таких как прямые и общие издержки, заработная плата персонала;
Условия финансирования;
Инвестиционный план проекта;
Условия лизинга (если имеется).
Выходами финансовой модели в Excel являются:
Отчет о прибыли и убытках;
Отчет о движении денежных средств;
Финансовые показатели проекта.
Модель линейной регрессии является часто используемой и наиболее изученной в эконометрике . А именно изучены свойства оценок параметров, получаемых различными методами при предположениях о вероятностных характеристиках факторов, и случайных ошибок модели. Предельные (асимптотические) свойства оценок нелинейных моделей также выводятся исходя из аппроксимации последних линейными моделями. Необходимо отметить, что с эконометрической точки зрения более важное значение имеет линейность по параметрам , чем линейность по факторам модели.
Регрессионная модель
где — параметры модели, — случайная ошибка модели, называется линейной регрессией, если функция регрессии имеет вид
где — параметры (коэффициенты) регрессии, — регрессоры (факторы модели), k — количество факторов модели.
Коэффициенты линейной регрессии показывают скорость изменения зависимой переменной по данному фактору, при фиксированных остальных факторах (в линейной модели эта скорость постоянна):
Параметр , при котором нет факторов, называют часто константой . Формально — это значение функции при нулевом значении всех факторов. Для аналитических целей удобно считать, что константа — это параметр при «факторе», равном 1 (или другой произвольной постоянной, поэтому константой называют также и этот «фактор»). В таком случае, если перенумеровать факторы и параметры исходной модели с учетом этого (оставив обозначение общего количества факторов — k), то линейную функцию регрессии можно записать в следующем виде, формально не содержащем константу:
где — вектор регрессоров, — вектор-столбец параметров (коэффициентов).
Линейная модель может быть как с константой, так и без константы. Тогда в этом представлении первый фактор либо равен единице, либо является обычным фактором соответственно
Проверка значимости регрессии
Критерий Фишера для регрессионной модели отражает, насколько хорошо эта модель объясняет общую дисперсию зависимой переменной. Расчет критерия выполняется по уравнению:где R - коэффициент корреляции;
f 1 и f 2 - число степеней свободы.
Первая дробь в уравнении равна отношению объясненной дисперсии к необъясненной. Каждая из этих дисперсий делится на свою степень свободы (вторая дробь в выражении). Число степеней свободы объясненной дисперсии f 1 равно количеству объясняющих переменных (например, для линейной модели вида Y=A*X+B получаем f 1 =1). Число степеней свободы необъясненной дисперсии f 2 = N -k -1, где N -количество экспериментальных точек, k -количество объясняющих переменных (например, для модели Y=A*X+B подставляем k =1).
Еще один пример:
для линейной модели вида Y=A 0 +A 1 *X 1 +A 2 *X 2 , построенной по 20 экспериментальным точкам, получаем f 1 =2 (две переменных X 1 и X 2), f 2 =20-2-1=17.
Для проверки значимости уравнения регрессии вычисленное значение критерия Фишера сравнивают с табличным , взятым для числа степеней свободы f 1 (бóльшая дисперсия) и f 2 (меньшая дисперсия) на выбранном уровне значимости (обычно 0.05). Если рассчитанный критерий Фишера выше, чем табличный, то объясненная дисперсия существенно больше, чем необъясненная, и модель является значимой.
Коэффициент корреляции и F -критерий, наряду с параметрами регрессионной модели, как правило, вычисляются в алгоритмах, реализующих
В целях исследований часто бывает удобно представить исследуемый объект в виде ящика, имеющего входы и выходы, не рассматривая детально его внутренней структуры. Конечно, преобразования в ящике (на объекте) происходят (сигналы проходят по связям и элементам, меняют свою форму и т. п.), но при таком представлении они происходят скрыто от наблюдателя.
По степени информированности исследователя об объекте существует деление объектов на три типа «ящиков»:
- «белый ящик» : об объекте известно все;
- «серый ящик» : известна структура объекта, неизвестны количественные значения параметров;
- «черный ящик» : об объекте неизвестно ничего.
Черный ящик условно изображают как на рис. 2.1 .
Значения на входах и выходах черного ящика можно наблюдать и измерять. Содержимое ящика неизвестно.
Задача состоит в том, чтобы, зная множество значений на входах и выходах, построить модель, то есть определить функцию ящика, по которой вход преобразуется в выход. Такая задача называется задачей регрессионного анализа .
В зависимости от того, доступны входы исследователю для управления или только для наблюдения, можно говорить про активный или пассивный эксперимент с ящиком.
Пусть, например, перед нами стоит задача определить, как зависит выпуск продукции от количества потребляемой электроэнергии. Результаты наблюдений отобразим на графике (см. рис. 2.2 ). Всего на графике n экспериментальных точек, которые соответствуют n наблюдениям.
наблюдения над черным ящиком
Для начала предположим, что мы имеем дело с черным ящиком, имеющим один вход и один выход. Допустим для простоты, что зависимость между входом и выходом линейная или почти линейная. Тогда данная модель будет называться линейной одномерной регрессионной моделью .
1) Исследователь вносит гипотезу о структуре ящика
Рассматривая экспериментально полученные данные, предположим, что они подчиняются линейной гипотезе, то есть выход Y зависит от входа X линейно, то есть гипотеза имеет вид: Y = A 1 X + A 0 (рис. 2.2 ).
2) Определение неизвестных коэффициентов A 0 и A 1 модели
Линейная одномерная модель (рис. 2.3 ).
Для каждой из n снятых экспериментально точек вычислим ошибку (E i ) между экспериментальным значением (Y i Эксп. ) и теоретическим значением (Y i Теор. ), лежащим на гипотетической прямой A 1 X + A 0 (см. рис. 2.2 ):
E i = (Y i Эксп. Y i Теор.), i = 1, , n ;
E i = Y i A 0 A 1 · X i , i = 1, , n .
Ошибки E i для всех n точек следует сложить. Чтобы положительные ошибки не компенсировали в сумме отрицательные, каждую из ошибок возводят в квадрат и складывают их значения в суммарную ошибку F уже одного знака:
E i 2 = (Y i A 0 A 1 · X i ) 2 , i = 1, , n .
![]()
Цель метода минимизация суммарной ошибки F за счет подбора коэффициентов A 0 , A 1 . Другими словами, это означает, что необходимо найти такие коэффициенты A 0 , A 1 линейной функции Y = A 1 X + A 0 , чтобы ее график проходил как можно ближе одновременно ко всем экспериментальным точкам. Поэтому данный метод называется методом наименьших квадратов .
Суммарная ошибка F является функцией двух переменных A 0 и A 1 , то есть F (A 0 , A 1) , меняя которые, можно влиять на величину суммарной ошибки (см. рис. 2.4 ).
 |
Чтобы суммарную ошибку минимизировать, найдем частные производные от функции F по каждой переменной и приравняем их к нулю (условие экстремума):
![]()
После раскрытия скобок получим систему из двух линейных уравнений:
![]()
![]()
Для нахождения коэффициентов A 0 и A 1 методом Крамера представим систему в матричной форме:

Решение имеет вид:


Вычисляем значения A 0 и A 1 .
3) Проверка
Чтобы определить, принимается гипотеза или нет, нужно, во-первых, рассчитать ошибку между точками заданной экспериментальной и полученной теоретической зависимости и суммарную ошибку:
E i = (Y i Эксп. Y i Теор.), i = 1, , n
![]()
И, во-вторых, необходимо найти значение σ по формуле , где F суммарная ошибка, n общее число экспериментальных точек.
Если в полосу, ограниченную линиями Y Теор. S и Y Теор. + S (рис. 2.5 ), попадает 68.26% и более экспериментальных точек Y i Эксп. , то выдвинутая нами гипотеза принимается. В противном случае выбирают более сложную гипотезу или проверяют исходные данные. Если требуется бо льшая уверенность в результате, то используют дополнительное условие: в полосу, ограниченную линиями Y Теор. 2S и Y Теор. + 2S , должны попасть 95.44% и более экспериментальных точек Y i Эксп. .
Расстояние S связано с σ следующим соотношением:
S = σ /sin(β ) = σ /sin(90° arctg(A 1)) = σ /cos(arctg(A 1)) ,
что проиллюстрировано на рис. 2.6 .
| Рис. 2.7. Иллюстрация закона нормального распределения ошибок |
Наконец, приведем на рис. 2.8 графическую схему реализации одномерной линейной регрессионной модели.
наименьших квадратов в среде моделирования
Линейная множественная модель
Предположим, что функциональная структура ящика снова имеет линейную зависимость, но количество входных сигналов, действующих одновременно на объект, равно m (см. рис. 2.9 ):
Y = A 0 + A 1 · X 1 + + A m · X m .
 |
черного ящика на схемах
Так как подразумевается, что мы имеем экспериментальные данные о всех входах и выходах черного ящика, то можно вычислить ошибку между экспериментальным (Y i Эксп. ) и теоретическим (Y i Теор. ) значением Y для каждой i -ой точки (пусть, как и прежде, число экспериментальных точек равно n ):
E i = (Y i Эксп. Y i Теор.), i = 1, , n ;
E i = Y i A 0 A 1 · X 1i A m · X mi , i = 1, , n .
Минимизируем суммарную ошибку F :
Ошибка F зависит от выбора параметров A 0 , A 1 , , A m . Для нахождения экстремума приравняем все частные производные F по неизвестным A 0 , A 1 , , A m к нулю:
![]()
Получим систему из m + 1 уравнения с m + 1 неизвестными, которую следует решить, чтобы определить коэффициенты линейной множественной модели A 0 , A 1 , , A m . Для нахождения коэффициентов методом Крамера представим систему в матричном виде:

Вычисляем коэффициенты A 0 , A 1 , , A m .
Далее, по аналогии с одномерной моделью (см. 3). «Проверка»), для каждой точки вычисляется ошибка E i ; затем находится суммарная ошибка F и значения σ и S с целью определить, принимается ли выдвинутая гипотеза о линейности многомерного черного ящика или нет.
При помощи подстановок и переобозначений к линейной множественной модели приводятся многие нелинейные модели. Подробно об этом рассказывается в материале следующей лекции.